tbf, the 2nd sum is exactly the first one just multiplied by 1/2. though i get that the progression is natural, even, and odd.
the last one is definitely
oddpuzzling, but i cannot intuitively get the first one. how does summing the inverse of triangular number equal 2?1/(n * (n+1)) = 1/n - 1/(n+1)
1/(1 * 2) + 1/(2 * 3) + 1/(3 * 4) + ... = 1 - 1/2 + 1/2 - 1/3 + 1/3 - 1/4 + ... = 1
Written a bit more explicitly (although I kinda handwaved away the final term--the point is that you end up with one unpaired term which goes to zero)
Show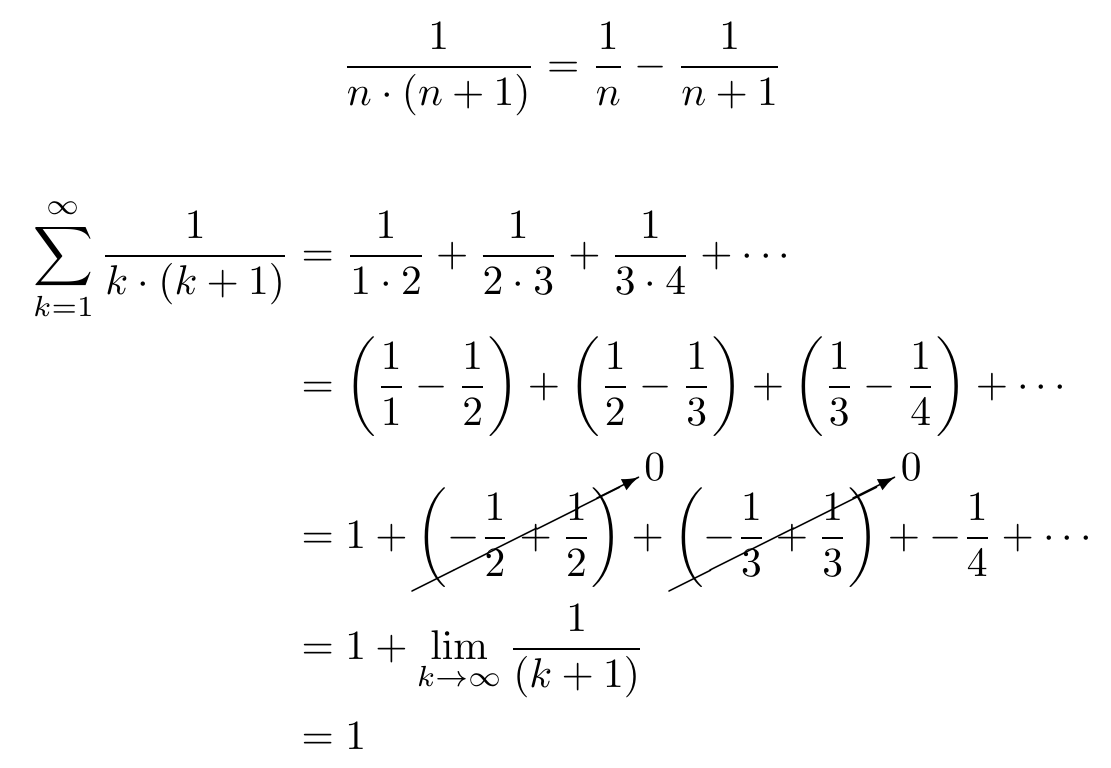
edit: I was honestly confused about how exactly this related to the question, but seeing the comment from @yetAnotherUser@discuss.tchncs.de (not visible from Hexbear) which showed that the first sum in the image is equivalent to
the sum from n = 1 to ∞ of 2/(n * (n + 1))
made things clear (just take the above, put 2 in the numerator, and you get a result of 2)
What's the big deal? Just solve for ...
... = (π^2 / 6) - (1 + 1/4 + 1/9)
Ez
/s


